The video discusses the collision of a point mass with a rod placed on a horizontal plane. It explains the conservation of linear and angular momentum to calculate the velocity of the center of mass and the angular velocity of the rod after the collision.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains how to solve for the angular velocity as a function of theta in an equation involving angular acceleration and angle. It demonstrates the use of differential kinematical equations and the process of integrating to find the solution.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
This video discusses the dynamics of a rod hinged at one point when released from rest, covering topics such as angular acceleration, velocity, and torque calculations.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video discusses how to calculate the forces and torque on a system involving a rigid body, taking into consideration the balance state of the system. It provides a step-by-step guide on how to calculate the unknown forces and torques acting on the rigid body and demonstrates the application of Newton's laws and the concept of torque in the calculation.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
This video demonstrates how to calculate torque using the position vector and force in vector notation. It goes through the step-by-step process of using the R cross F formula to find the torque experienced by a point mass with respect to an axis. The video also discusses the use of different formulas, the matrix method for cross product calculations, and the direction of torque using the unit vector.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
This video explains how to calculate torque and its direction, starting with the calculation of torque for a point mass, and then moving on to the calculation of torque for rigid bodies. It also covers the magnitude and direction of torque, and provides tips for faster calculation of torque direction.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains the Perpendicular Axis Theorem, which is used to calculate the moment of inertia for a body about multiple perpendicular axes. It outlines the conditions for applying the theorem and demonstrates the relationship between the three mutually perpendicular axes. The video also goes into the mathematical calculations involved in determining the moment of inertia for each axis.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
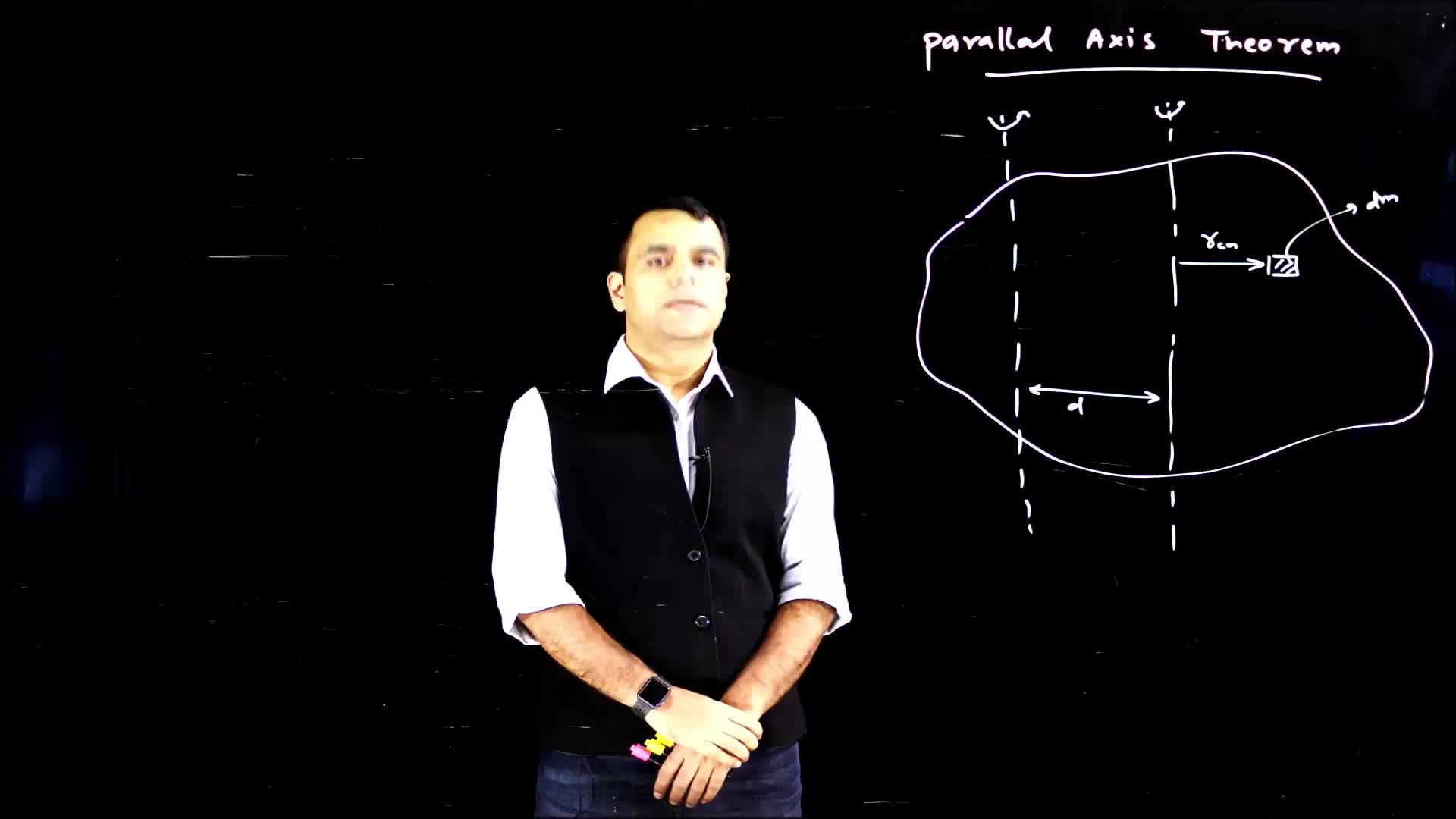
This video explains the parallel axis theorem in physics, which provides a relationship between the moment of inertia for the same body about two parallel axes. The video also discusses the conditions for using the theorem and the significance of the relationship between the moment of inertia for the axis passing through the center of mass and other parallel axes.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video discusses the calculation of the angular momentum of a disk rolling on a rough surface, with its center of mass moving at velocity V and an angular velocity of omega. The angular momentum is calculated about a point P, which is the bottommost point of the disk. The process involves converting the rigid body into two separate systems, placing a hinge at the axis, and calculating the R cross pcm and ICM omega components separately before adding them to determine the angular momentum of the disk.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
Explanation of the process to calculate the moment of inertia for a solid sphere using the concept of hollow spheres as the element. The process includes defining the mass and radius of the hollow sphere element, calculating the moment of inertia for the element, and integrating to obtain the moment of inertia for the entire solid sphere.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
This video explains the process of calculating the angular momentum of a point mass in projectile motion after a certain amount of time. It includes the kinematic equations, velocity calculations, and the use of the formula for maximum height in projectile motion to determine the angular momentum. The video provides a step-by-step explanation of the calculation process.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
Understanding the process of calculating the moment of inertia for a hollow sphere and the integration involved in the process.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains the process of calculating the moment of inertia for a solid cylinder. It covers the derivation of the formula and the integration required to find the moment of inertia for the entire body.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains how to calculate the torque applied to a point mass along the x-axis, given the force and angle of application. It discusses the various methods of calculating torque and demonstrates a specific method for the given scenario. It also explains how to determine the direction of torque. The video concludes by emphasizing that following the correct method will always yield the same result.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
Calculating the minimum velocity required for a point mass to bring a system to a horizontal position after a collision.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
This video explains the process of calculating the moment of inertia for a hollow cylinder. It covers the method of cutting the cylinder into elements, calculating the mass and moment of inertia for each element, and integrating to find the moment of inertia for the entire cylinder.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains the rotation of a fan and how to calculate the time it takes for the angular velocity to become half of the maximum speed. The constant angular acceleration is used to solve the problem.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video discusses the process of calculating the moment of inertia for a disk with the axis passing through the center of mass, using ring-shaped elements. The method involves calculating the mass of the ring and then the moment of inertia of the element about the axis. The total moment of inertia for the entire disk is obtained through integration.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains the process of calculating the moment of inertia for a ring element about an axis perpendicular to the plane of the ring and passing through the center of mass. It covers the use of circular variables, the calculation of mass, and the formula for moment of inertia for the ring element
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
Explanation of how to calculate the angular momentum for a symmetrical body given the moment of inertia and angular velocity, including the conversion of angular velocity from revolutions per second to radians per second.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
Lecture on the calculation of moment of inertia for a rod with mass M and length L, using point elements and integration.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains how to calculate the moment of inertia for a rod when the axis is passing through the rod itself. It goes through the process of calculating the moment of inertia for the entire rod and explains why it is equal to zero in this specific case.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video discusses the calculation of the moment of inertia for a linear rod about an axis that is perpendicular to the rod and passes through one of its corners. The process involves dividing the rod into elements, calculating the moment of inertia for each element, and then integrating to find the total moment of inertia for the entire rod.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video discusses the calculation of the moment of inertia for a disk about different axes using the perpendicular axis theorem and parallel axis theorem.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
The video explains how to calculate the moment of inertia for a ring about a specific axis using the parallel axis theorem.
|
|
|||
|
|
|||
|
|
|
|
|
Uploaded
|
|
0:00 |
|
|
|
|
0:05 | ||
|
|
0:10 |
|
|
|
|
0:15 | ||
|
|
0:20 | ||
|
|
0:25 |
|
|
|
|
0:30 | ||
